WTH – der Schlüssel zu präzisen Temperaturmessungen in der Industrie
Sie wissen noch nicht, wie ein WTH-Sensor funktioniert oder welcher Sensortyp am besten zu Ihrer jeweiligen Anwendung passt? Keine Sorge – wir sind gerne für Sie da! In diesem Wissensartikel stellen wir Ihnen die am häufigsten eingesetzten WTH-Typen, ihre Bauweise und ihre Vor- und Nachteile vor. Los geht´s.
Das Wichtigste zuerst
Bei WTHs aus Platin wird die Buchstabenkombination „Pt“ vorangestellt, gefolgt von einer Nummer, die für den Nennwiderstand bei 0 Grad C steht, beispielsweise Pt100.
Dies sind die am häufigsten verwendeten WTH-Typen in industriellen Anwendungen und das aus gutem Grund. Diese Geräte sind bei Überwachungsanwendungen im empfohlenen Bereich in der Regel genauer und können eine größere Stabilität als Thermoelemente oder andere Temperaturfühler vorweisen.
Nachdem Sie nun wissen, was ein WTH ist, werfen wir einen Blick auf die drei häufigsten WTH-Typen (aus Platin, Nickel oder Kupfer) und wie sie sich voneinander unterscheiden. Sie sind allerdings auch die kostspieligste Ausführung.
Platin-WTH
Bei WTHs aus Platin wird die Buchstabenkombination „Pt“ vorangestellt, gefolgt von einer Nummer, die für den Nennwiderstand bei 0 Grad C steht, beispielsweise Pt100.
Dies sind die am häufigsten verwendeten WTH-Typen in industriellen Anwendungen und das aus gutem Grund. Das rührt daher, dass Platin eine hervorragende Korrosionsbeständigkeit und eine ausgezeichnete Langzeitstabilität vorweisen und darüber hinaus auch einen breiten Temperaturbereich (-200…+850°C) abdecken kann. Sie sind allerdings auch die kostspieligste Ausführung.
Nickel-WTH
Bei Nickel WTHs wird die Buchstabenkombination „Ni“ vorangestellt, gefolgt von einer Nummer, die für den Nennwiderstand bei 0 Grad C steht, beispielsweise Ni120.
Diese Varianteist günstiger als die Platin-Variante und hat einen guten Korrosionswiderstand. Nickel altert allerdings mit der Zeit schneller und büßt bei höheren Temperaturen an Genauigkeit ein. Nickel ist auf einen Messbereich von -80…+260°C beschränkt.
Kupfer-WTH
Bei Kupfer-WTHs wird die Buchstabenkombination „Cu“ vorangestellt, gefolgt von einer Nummer, die für den Nennwiderstand bei 0 Grad C steht, beispielsweise Cu10.
Diese weisen von den drei WTH-Typen die beste Linearität zwischen Widerstand und Temperatur auf, und Kupfer ist ein kostengünstiges Material. Darüber hinaus ist Kupfer ein preiswertes Material. Kupfer beginnt allerdings bei höheren Temperaturen, zu rosten. Kupfer ist auf einen Messbereich von -200…+260°C beschränkt.
Wie werden WTH gebaut?
Es gibt drei Bauweisen für Widerstandstemperatursensoren: Wire wound RTDs, coiled element RTDs, and thin film RTDs. Wir werden alle Bauweisen im Folgenden separat behandeln.
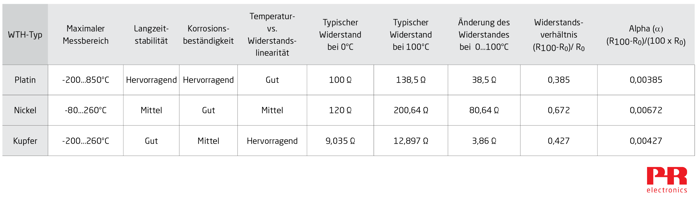
Drahtgewickelte WTH
Zunächst einmal gibt es die drahtgewickelten WTH. In diesem Fall wird ein Widerstandsdraht um einen nichtleitenden Kern gewickelt, der meist aus Keramik besteht. Dabei schneidet der Sensorhersteller die Länge des Widerstandsdrahts sorgfältig zu, um den angegebenen Widerstand bei 0 °C zu erreichen. Dies wird als „R0“-Widerstand bezeichnet.
Im nächsten Schritt wird ein Anschlussdraht mit dem Widerstandsdraht verbunden und anschließend wird zum Schutz des Drahtes eine Glas- oder Keramikbeschichtung aufgebracht. Mit steigender Temperatur vergrößert sich auch die Länge des Widerstandsdrahtes leicht. Bei der Entwicklung muss darauf geachtet werden, dass sich der Widerstandsdraht bei steigenden Temperaturen nicht verdreht oder anderweitig verformt. Das ist darauf zurückzuführen, dass mechanische Beanspruchungen zu einer Veränderung des Drahtwiderstandes führen.
WTH in Laborqualität, die in Kalibrier- oder Normlaboren zum Einsatz kommen, beseitigen diese Fehlerquelle dadurch, dass der Widerstandsdraht lose um eine nicht leitfähige Stützkonstruktion gewickelt wird. Diese WTH-Variante ist äußerst genau, aber auch sehr empfindlich und daher für die meisten Industrieanwendungen ungeeignet.
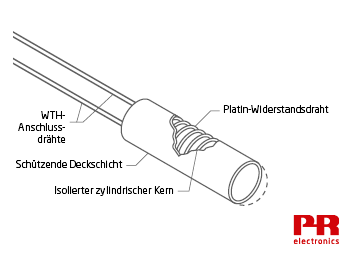
Gewickelte WTH
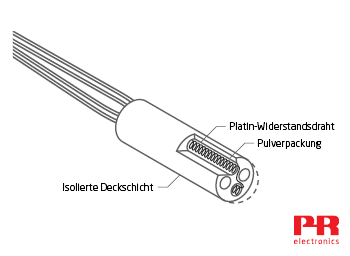
Die gewickelte WTH ist die zweite Bauweise: Der Widerstandsdraht wird zu kleinen Spulen gerollt, die lose in eine Keramikform passen, die dann mit nichtleitendem Pulver gefüllt wird.
Der Widerstandsdraht kann sich bei Temperaturveränderungen nach Bedarf ausdehnen und zusammenziehen und minimiert daher die durch mechanische Belastung verursachte Fehlerquote. Das Pulver erhöht den Anteil der Wärmübertragung in die Spulen und verbessert auf diese Weise die Ansprechzeit. Die gewickelten WTH sind normalerweise durch einen Metallmantel geschützt und für Industrieanwendungen geeignet.
Dünnschicht-WTH
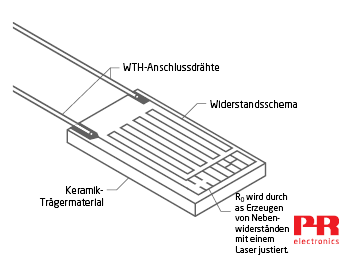
Und letztendlich gibt es noch die Dünnschicht-WTHs. Sie werden in Massenproduktion hergestellt und kosten weniger als die anderen WTH-Typen. Sie sind kleiner und haben eine kürzere Ansprechzeit als die anderen Modelle, was bei vielen Anwendungen wünschenswert ist. Bei ihrer Herstellung wird eine dünne Platinschicht auf eine Keramikunterlage aufgebracht.
Der Hersteller stellt den Widerstand auf 0°C ein, indem mit einem Laserstrahl parallele Nebenwiderstände in dieser Schicht erzeugt werden. Je mehr Nebenwiderstände erzeugt werden, desto höher ist der Widerstand bei 0°C. Dünnschicht-WTH messen aus folgenden Gründen nicht so genau wie die anderen Varianten:
- Der R0-Widerstand kann nicht so genau eingestellt werden, wie bei den anderen Ausführungen.
- Die Keramikunterlage und die Platinbeschichtung haben leicht unterschiedliche Ausdehnungsraten. Das führt bei höheren Temperaturen zu einem Belastungsfehler.
- Da die Dünnschicht-WTH kleiner sind, verursacht der WTH-Erregungsstrom eine leicht erhöhte Fehlerrate aufgrund der Eigenerwärmung des WTH.
Verdrahtungskonfigurationen von WTH
Widerstandsthermometer können als 2-, 3- oder 4-Draht-Konfigurationen ausgeführt werden, von denen jede unterschiedliche Vorteile bietet:
- 2-Draht-Konfiguration: Diese einfachste und kostengünstigste Variante eignet sich vor allem für kurze Distanzen, bei denen sich der Widerstand der Anschlussdrähte nicht nennenswert auf die Genauigkeit auswirkt. Sie kommt in der Regel in Industrieanwendungen zum Einsatz, bei denen eine hohe Genauigkeit zweitrangig ist.
- 3-Draht-Konfiguration: Die am häufigsten verwendete Konfiguration gleicht den von den Drähten selbst verursachten Widerstand aus, der zu einer Verzerrung der Temperaturmesswerte führen kann. Diese Konfiguration kommt vor allem dann zum Einsatz, wenn eine höhere Genauigkeit über moderate Distanzen hinweg gefragt ist.
- 4-Draht-Konfiguration: Diese Konfiguration bietet die höchste Genauigkeit und beseitigt gleichzeitig den Einfluss des Drahtwiderstands. Sie ist optimal für Präzisionsmessungen in Laboren und bei Anwendungen geeignet, in denen es um höchste Genauigkeit geht.
Das Verständnis dieser Konfigurationen ist wesentlich, um ausgehend von den spezifischen Anforderungen einer Anwendung die optimale WTH-Konfiguration auswählen zu können, die die richtige Kombination aus Kosten, Bequemlichkeit und Genauigkeit bietet.
WTH-Widerstandsverhältnis
Der Begriff „Widerstandsverhältnis“ beschreibt die durchschnittliche Steigung der Temperatur gegenüber der des Widerstandes, während die WTH-Temperatur von 0°C auf +100°C steigt. Die Formel für das Widerstandsverhältnis lautet wie folgt:
(R100-R0) / R0
Wobei:
R100 = WTH-Widerstand bei 100°C.
R0 = WTH-Widerstand bei 0°C.
Das Widerstandsverhältnis wird von der Art und der Reinheit des Metalls beeinflusst, aus dem das WTH hergestellt wird. WTH mit einem hohen R0-Wert in Verbindung mit einem hohen Widerstandsverhältnis sind im Allgemeinen leichter zu messen. Dennoch beeinflussen auch andere Eigenschaften des Metalls im Widerstandsdraht die inhärente Genauigkeit des WTH.
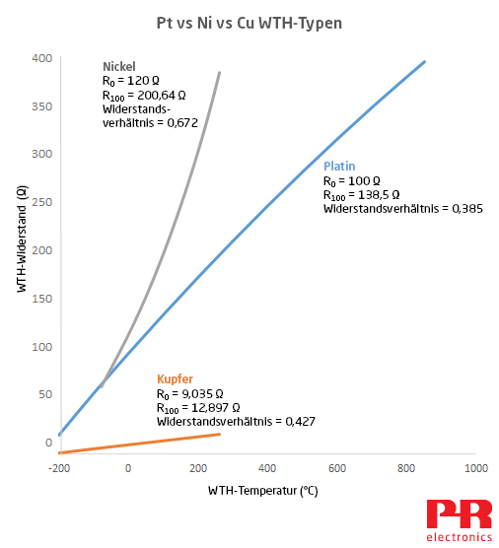
Die in Industrieanwendungen verwendeten Platin-WTH entsprechen normalerweise der Norm IEC 60751. Diese WTH verfügen über ein Widerstandsverhältnis von (138,5 Ω - 100 Ω)/100 Ω = 0,385 Ω/°C. Bei den gängigen Industrieanwendungen ist diese WTH-Variante durch einen Edelstahlmantel geschützt.
Bei WTH-Standards für den Laboreinsatz kommt Platin mit einem höheren Reinheitsgrad und einem höheren Widerstandsverhältnis zum Einsatz: (139,2 Ω - 100 Ω)/100 Ω = 0,392 Ω / °C. Bei Temperaturen über +670°C wird das hochreine Platin durch Metallionen verunreinigt, die von der Edelstahlsonde freigesetzt werden, was zu einer Änderung des Widerstandsverhältnisses führt. Aus diesem Grund werden diese WTH durch eine Sonde aus Quarzglas oder Platin geschützt. Diese Sondenmaterialien verhalten sich bei hohen Temperaturen inert, sodass das WTH vor Verunreinigung geschützt ist.
Nickel-WTH gemäß DIN 43760 haben ein Widerstandsverhältnis von (161,7805 Ω – 100 Ω)/100 Ω = 0,618 Ω / °C. Nickel-WTH, die normalerweise in den USA zum Einsatz kommen, haben ein Widerstandsverhältnis von (200,64 Ω – 120 Ω)/120 Ω = 0,672 Ω / °C (in der Grafik oben dargestellt).
Kupfer-WTH[1] sind mit folgenden Werten erhältlich: R0 = 9,035 Ω oder 100 Ω. Beide Varianten haben ein Widerstandsverhältnis von 0,427:
(12,897 Ω - 9,035 Ω) / 9,035 Ω = 0,427 Ω / °C.
(142,7 Ω – 100 Ω) / 100 Ω = 0,427 Ω / °C.
Nickel- oder Kupfer-WTH? Die jeweiligen Vorteile
Nickel erzeugt einen hohen Widerstand bei 0°C und verfügt über ein hohes Widerstandsverhältnis. Dadurch ist dieses empfindliche WTH einfach zu messen. Dank dieser Eigenschaften können auch Fehler aufgrund von Anschlussdrahtwiderstand auf ein Minimum reduziert werden. Bei einem WTH beträgt die ungefähre Fehlerquote aufgrund des Anschlussdrahtwiderstandes:
Anschlussdrahtwiderstand / (R100-R0) x 0,01
Zum Beispiel:
Ein 2-Draht-Nickel-WTH misst die Temperatur eines Luftkanals. Jeder Anschlussdraht hat einen Widerstand von 0,25 Ω, das entspricht einem Gesamtwiderstand des Anschlussdrahtes von 0,5 Ω.
Der durch den Anschlussdrahtwiderstand hervorgerufene Fehler kann daher wie folgt berechnet werden:
0,5 Ω / (161,78 – 100) x 0,01 = 0,81°C. Das ist für viele Anwendungen genau genug.
Im Vergleich dazu die Werte einer 2-Draht-Platin-WTH mit demselben Anschlussdrahtwiderstand:
0,5 Ω / (138,5 – 100) x 0,01 = 1,3°C.
Aufgrund der hohen Empfindlichkeit des Nickel-WTH, kann dieses WTH von einem preiswerten Messumformer mit geringer Präzision mit einer akzeptablen Genauigkeit gemessen werden. Nickel-WTH sind in HLK-Anlagen und anderen preissensiblen Anwendungen zu finden.
Kupfer-WTH haben dieselbe Wärmeausdehnungsrate und elektromagnetische Hysterese wie Kupferwicklungen, die in Elektromotoren und Generatoren Verwendung finden. Aus diesem Grund werden Kupfer-WTH manchmal auch zur Temperaturmessung von Wicklungen verwendet.
Darüber hinaus kann Kupfer ein außergewöhnlich lineares Verhältnis zwischen Temperatur und Widerstand vorweisen. Daher ist es auch möglich, eine enge Temperaturspanne ohne zusätzliche Linearisierung genau zu messen.
Zum Beispiel:
Ein Cu100-WTH erzeugt bei 0°C einen Widerstand von 100 Ω und bei 100°C einen Widerstand von 142,743 Ω. Eine lineare Extrapolation ergibt den folgenden theoretischen Widerstand bei 50°C: (R100 – R0)/2 + R0
= (142,743 – 100)/2 + 100 = 121,3715 Ω
Veröffentlichten Tabellen zum Verhältnis zwischen Widerstand und Temperatur zufolge, erzeugt das WTH einen Widerstand von 121,3715 Ω bei 50°C, sodass das WTH zwischen 0…+100°C funktional linear verläuft.
Die Nichtlinearität von Kupfer tritt erst beim Messen einer breiten Spanne zutage. Bei einer Messung zwischen 0….200°C ergibt die lineare Extrapolation bei 100°C beispielsweise einen theoretischen Widerstand von (185,675 – 100)/2 + 100 = 142,838 Ω. Den Tabellen zufolge liegt der WTH-Widerstand bei 100°C jedoch bei 142,743 Ω.
Die Differenz von +0,095 Ω in °C: 0,095 Ω / 0,427 Ω pro Grad = ein Fehler von +0,222°C
WTH-Toleranz
Die meisten Sensor-Hersteller produzieren Platin-WTH mit Genauigkeitsgraden, die den WTH-Normen IEC 60751 oder ASTM E1137 entsprechen.
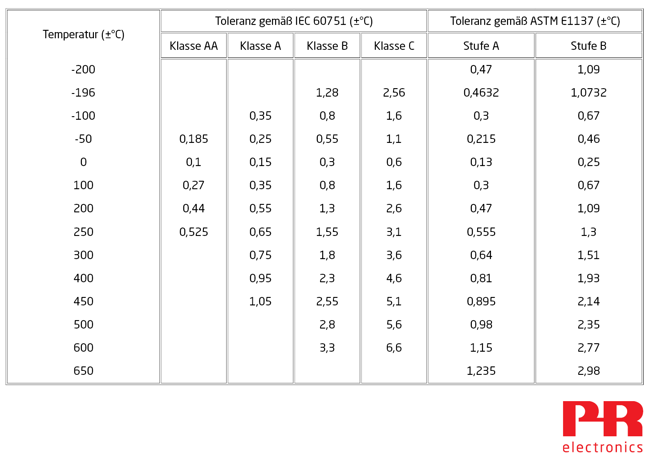
Die Norm IEC 60751 legt vier Toleranzklassen fest: Klasse AA, A, B und C. Die Norm ASTM E1137 legt zwei Toleranzklassen fest: Klasse A und B.

Bitte beachten Sie, dass IEC 60751 einen maximalen Temperaturbereich für jede Klasse festlegt. So muss ein Sensor der Klasse A, der mit einem gewickelten WTH-Element ausgestattet ist, beispielsweise die vorgegebene Toleranz von -100…+450°C einhalten. Wenn der Sensor außerhalb dieses Temperaturbereichs betrieben wird, entspricht die Sensorgenauigkeit eventuell Klasse B.
Sensoren der Toleranzstufe A oder B gemäß ASTM E1137 müssen die vorgegebene Toleranz von -200…+650°C einhalten.
Die folgende Tabelle zeigt die berechnete Toleranz für jede WTH-Klasse oder -Stufe. Bitte beachten Sie, dass WTH der Klasse C bei 600°C einen großen Toleranzbereich von ±6.6°C haben. Für die meisten Industrieanwendungen sind WTH mit einer Toleranz der Klasse B oder besser erforderlich.
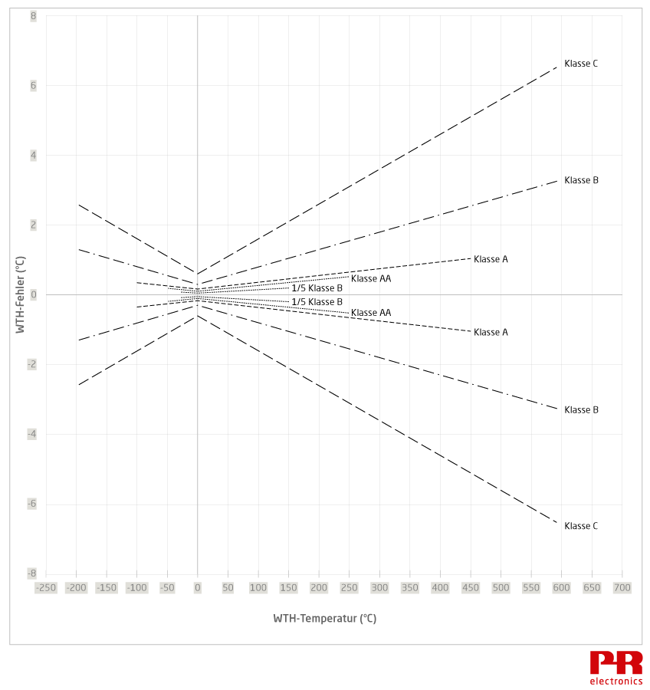
Die folgende Grafik zeigt die Toleranz der WTH, die IEC 60751 erfüllen. Daraus ergibt sich, dass die Genauigkeit der WTH bei 0°C am größten ist. Bei Temperaturen oberhalb oder unterhalb von 0°C ist die Fehlerquote höher.
Callendar-Van-Dusen-Gleichungen
Die Callendar-Van-Dusen-Gleichungen beschreiben das Verhältnis zwischen Temperatur und Widerstand bei industriellen Platin-WTH. Es gibt zwei Callendar-Van-Dusen-Gleichungen:
Bei Temperaturen < 0°C beträgt der WTH-Widerstand bei einer bestimmten Temperatur:
Rt = R0[1 + At + Bt² + C (t - 100) t³]
Bei Temperaturen ≥ 0°C beträgt der WTH-Widerstand bei einer bestimmten Temperatur:
Rt = R0(1 + At + Bt²)
Die Koeffizienten A, B, C sowie α, δ, β sind bei jedem WTH einzigartig. Die folgenden Werte gelten für die WTH gemäß den Normen IEC 60751 und ASTM E1137:
A = 3,9083 x 10-3
B = -5,775 x 10-7
C = -4,183 x 10-12
α = 3,85 x 10-3 *
β = 1,5°C
δ = 0,1086
* “α” ist die „Alpha”-Konstante. Bei Alpha handelt es sich um das Widerstandsverhältnis/100:
α = (R100 – R0) / (100 x R0).
Der Alpha-Wert einer Platin-WTH nach Maßgabe von IEC 60751 beläuft sich auf:
(138,5 – 100) / (100 x 100)
= 0,00385
Nickel-WTH haben einen Alpha-Wert von:
0,672 / 100 = 0,00672.
Kupfer-WTH haben einen Alpha-Wert von:
0,427 / 100 = 0,00427.
Profitieren Sie von überragender Messgenauigkeit dank WTH-Charakterisierung
Auch qualitativ hochwertige WTH entsprechen nicht genau der W:T-Kurve gemäß IEC 60751/ASTM E1137. Zur weiteren Verbesserung der Messgenauigkeit kann eine WTH in einem Kalibrierlabor „charakterisiert“ werden. Das erfolgt durch eine sorgfältige Messung des WTH-Widerstandes bei unterschiedlichen Temperaturen und der anschließenden Ermittlung der Koeffizienten α, δ, β und A, B und C.
Mit diesen Koeffizienten können der 5437 2-Draht-HART 7 Temperaturmessumformer, der 5337 2-Draht Transmitter mit HART Protokoll, der 6337 2-Draht HART-Messumformer und der 6437 2-Draht-HART 7 Temperaturmessumformer programmiert werden. Auf diese Weise kann der Messumformer für eine außergewöhnliche Messgenauigkeit exakt an ein charakterisiertes WTH angepasst werden.
Sie sind nun bestens über alles Wissenswerte zur Auswahl des optimalen WTH für Ihre Anwendung und die Funktionsweise des jeweiligen WTH informiert. Haben Sie noch Fragen? Wir sind gerne für Sie da. Wir stehen Ihnen im Hinblick auf Ihre individuellen WTH-Anforderungen jederzeit mit Rat und Tat zur Seite.
Zurück zur PR-Wissensbibliothek
[1] HINWEIS: Ein Cu100-WTH hat einen höheren R100-R0-Wert und ist einfacher zu messen als das Cu9.035-WTH.
Geben Sie zwei Werte ein und berechnen Sie den WTH-Widerstand einer beliebigen Platin-WTH.




